Fishers Exact Test Continuous or Categorical
Introduction
When the conditions for Pearson's chi-square test are not met, especially when one or more of the cells have expi < 5 or with 2 × 2 contingency tables, an alternative approach is to use Fisher's exact test. Since this method is more computationally intensive, it is best used for smaller samples.
2 × 2 Contingency Table Example
Example 1: Repeat Example 2 from Independence Testing using the data in range A5:D8 of Figure 1; i.e. determine whether the cure rate is independent of the therapy used.
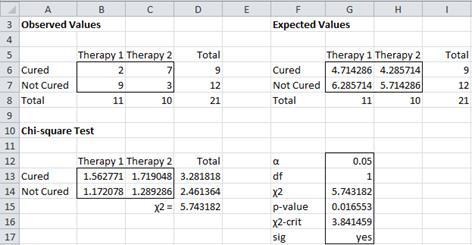
Figure 1 – Data and Chi-square test for Example 1
As you can see from Figure 1, the expectation for two of the cells (G6 and H6) is less than 5. Since we are dealing with a 2 × 2 contingency table with a relatively small sample size, it is better to use Fisher's exact test.
Fisher's exact test calculates how many different ways the above marginal frequencies can be achieved and then determines the probability that the above-observed cell configuration can be obtained merely by chance.
We can restrict our attention to any one of the cells since once the frequency for one cell is determined, the frequencies for the other cells can be determined from the marginal totals. We choose cell B6 since it has the smallest marginal total (namely 9 in cell D6) and its value is smaller than the other element that makes up this marginal total (namely 7 in cell C6).
Now cell B6 can take any value between 0 and 9; once this value is set the values of the other three cells can be adjusted to maintain the marginal totals.
Calculating the probabilities
The probability that cell B6 takes on a specific value x is equivalent to the probability of getting x successes in a sample of size 9 (cell D6) taken without replacement from a population of size 21 (cell D8) that contains 11 (cell B8) successful choices. This can be calculated by the hypergeometric distribution. Here cells D6 and B8 are cells with the marginal totals corresponding to cell B6 and cell D8 contains the grand total.
Figure 2 contains a table of the probabilities for each possible value of x.
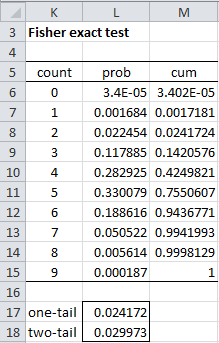
Figure 2 – Fisher exact test for Example 1
Excel formulas used
Thus, e.g., cell L11 contains the pdf value for the count in cell K11 as calculated by the formula
=HYPGEOM.DIST(K11,$B$8,$D$6,$D$8,FALSE)
As observed in Hypergeometric Distribution, the roles of marginal totals B8 and D6 can be interchanged in the above formula.
Users of Excel prior to Excel 2010 can employ the following formula instead
=HYPGEOMDIST(K11,$B$8,$D$6,$D$8)
Cell M11 contains the corresponding cdf value for the value in cell K11 via the formula
=HYPGEOM.DIST(K11,$B$8,$D$6,$D$8,TRUE)
Since a formula for the cdf is not available in Excel prior to Excel 2010, users of these versions of Excel can insert the formula = L6 into cell M6, the formula =L7+M6 into cell M7, and then highlight the range M7:M15, and press Ctrl-D. Cell M11 will now contain the cdf value for the value in cell K11 via the formula =M10+L11.
Analysis
The Fisher exact test consists of determining whether the probability is less than .05 that at most 2 of those taking therapy 1 are cured (the observed count in cell B6). From cell L17 of Figure 2, we see that the cdf at 2 is .024172 < .05 = α, and so we reject the null hypothesis and conclude there is a significant difference between the cure rates for the two therapies.
There are one-tail and two-tail versions of the test. The p-value for the one-tail test (cell L17) is given by the formula =SUM(L6:L8) or equivalently (for versions of Excel starting with Excel 2010)
= HYPGEOM.DIST(K8,B8,D6,D8,TRUE)
The p-value for the two-tail test (cell L18) is given by the formula
=SUM(L6:L8)+SUM(L14:L15)
where K14 is the leftmost cell in the right tail that has a pdf value ≤ L8 (since .005614 ≤ .022454, but .050522 > .022454). Equivalently, we can use the formula (for versions of Excel starting with Excel 2010)
= HYPGEOM.DIST(K8,B8,D6,D8,TRUE)+1− HYPGEOM.DIST(K13,B8,D6,D8,TRUE)
Worksheet Function
Real Statistics Excel Function: The Real Statistics Resource Pack provides the following worksheet function.
FISHERTEST(R1, tails) = the p-value calculated by the Fisher Exact Test for a 2 × 2, 2 × 3, 2 × 4, 2 × 5, 2 × 6, 2 × 7, 2 × 8, 2 × 9, 3 × 3, 3 × 4 or 3 × 5 contingency table contained in R1.
R1 must contain only numeric values. When R1 contains a 2 × 2 contingency table, there is an optional second argument, tails = 1 (one-tailed test) or 2 (two-tailed test, default). For contingency tables of other sizes, only the p-value of the two-tailed test can be returned.
For Example 1, FISHERTEST(B6:C7,1) = .024172 and FISHERTEST(B6:C7, 2) = .029973.
Limitations
Because the Fisher exact test can be resource-intensive, limits have been placed on the sum of all the cells in the supported contingency tables. These limits are currently set at 2,000 for a 2 × 3 table, 1,250 for a 2 × 4 table, 360 for a 2 × 5 table, 175 for a 2 × 6 table, 110 for a 2 × 7 table, 75 for a 2 × 8 table, 40 for a 2 × 9 table, 320 for a 3 × 3 table, 95 for a 3 × 4 table and 30 for a 3 × 5 table. There are no limits for 2 × 2 tables.
If you want to exceed these limits, you can add a third argument to the FISHERTEST function which specifies how much you want to increase the limit. E.g. if you want to use the Fisher exact test for a 3 × 3 contingency table in range A1:C3 the sum of whose cells is 350, then you can use the array formula =FISHERTEST(A1:C3,,1.1). The 1.1 specifies that you have increased the limit for a 3 × 3 contingency table from 320 to 320 × 1.1 = 352.
Since 350 < 352, the function will run, although it will take a little longer. Similarly, you can use =FISHERTEST(A1:C3,,1.5) for any 3 × 3 contingency table whose entries sum to at most 320 × 1.5 = 480. When the sum is 480, expect the processing to take some time.
3 × 2 Contingency Table Example
Example 2: Determine whether being pro-choice or pro-life is independent of a US citizen's political party based on the sample shown in range A3:D7 of Figure 3.
You can perform the Fisher exact test by using the worksheet formula =FISHERTEST(B4:C6). The result, as shown in cell H13 of Figure 3, is that being pro-choice or pro-life is not independent of party affiliation since p-value = 4.574E-06 < .05 = α (two-tailed test).

Figure 3 – Fisher exact test for Example 2
Data Analysis Tool
We can also use the Real Statistics Chi-square Test for Independence data analysis tool to get the same result by checking the Fisher Exact Test option in the dialog box that appears (as shown in Figure 3 of Chi-square Test for Independence).
Mid p-value correction
The Fisher Exact Test for 2 × 2 contingency tables can be viewed as too conservative. To address this issue, you can employ what is called the mid p-value correction.
To apply this correction for Example 1, you need to subtract half of the value in cell L8 of Figure 2 from the p-value calculated. This results in a p-value for the one-tail test of .012945 (i.e. .024172 – .022454/2) and .018746 (i.e. .029973 – .022454/2) for the two-tail test.
Real Statistics Function: The Real Statistics Resource Pack provides the following function:
FISHER_MIDP(R1, ) = the mid p-value for the 2 × 2 contingency table contained in R1. tails = 1 or 2 (default)
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2012) Fisher's exact test
https://en.wikipedia.org/wiki/Fisher%27s_exact_test
Ghent, A. W. (1972) A method for exact testing of 2×2, 2×3, 3×3, and other contingency tables, employing binomial coefficients
https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.135.4796&rep=rep1&type=pdf
Freeman, G. H. and Halton, J. H. (1951). Note on exact treatment of contingency, goodness-of-fit and other problems of significance. Biometrika, 38, 141-149.
https://academic.oup.com/biomet/article-abstract/38/1-2/141/245705?redirectedFrom=fulltext
Agresti, A. (2007) Introduction to categorical data analysis. 2nd Ed. Wiley
https://mregresion.files.wordpress.com/2012/08/agresti-introduction-to-categorical-data.pdf
Source: https://www.real-statistics.com/chi-square-and-f-distributions/fishers-exact-test/
0 Response to "Fishers Exact Test Continuous or Categorical"
Post a Comment